ovvero: il blog di Tommaso Correale Santacroce (pagina personale dell'autore)

Scrivi a
le tue osservazioni o le tue segnalazioni: saranno riportate in questo blog.
Il feed RSS di questo blog: 
|
|
| |
|
|
| |
Perché questo blog si chiama
"Quel che poi un metal detector..." ?
Poi la notte, in quelle poche ore in cui l'aereoporto rimane chiuso, in cui le grandi sale restano completamente sgombre e gli altoparlanti restano silenziosi, i metal detector stanno come monoliti in fila e raccontano... [ continua ]
|
|
|
|

Quel che poi un metal detector...
|
|
| |
20030527
Vedo foglie o triangoli?
Permalink (da utilizzare per segnalare questo post)

Con Franco Citterio, creatore di teste di legno (ma non solo) per le marionette della Compagnia Carlo Colla e figli, ci siamo più volte trovati a discutere se, scolpendo, lui avesse in mente precisamente il viso che voleva produrre o se avesse in mente qualcosa di più astratto, ovvero a quale geometria si riferisse per impostare i volumi di pieno e vuoto di una faccia che doveva si essere simile ad un volto umano ma scostarsene quel tanto da essere testa di marionetta. Mi ricordo che mi rispondeva: in fin dei conti l’abbozzo lo faccio su sfere, cubi, figure euclidee. Parlavamo dei frattali, ma la costruzione mentale del viso si appoggiava, prima di rendersi più complessa, alle forme semplici che avevamo studiato a scuola.
Nel 1975 Benoît Mandelbrot pubblica un libro scientifico, che vuole essere più divulgativo che dimostrativo, in cui presenta un gruppo di “mostri matematici” come rappresentanti di una nuova geometria: il titolo del libro è Les objets fractals ( ed it.: “Gli oggetti frattali. Forma, caso e dimensione”, Einaudi Paperbacks 173, 987) e la nuova geometria è appunto chiamata Frattale.
L’intenzione di Mandelbrot non è tanto quella di sviscerare invenzioni matematiche più o meno famose fino ad allora reiette dal mondo scientifico (considerate anomalie), quanto presentare un’idea: la possibilità di utilizzare procedimenti matematici fino ad allora considerati “impossibili” per creare modelli di qualcosa normalmente considerata non misurabile geometricamente: la natura.
Così la sua carrellata di “disgustose piaghe”, come vennero talvolta chiamati le teorie matematiche anomale, fa scorrere lo sguardo su oggetti e dimensioni differenti: dalla frequenza delle galassie nello spazio, alla misurazione delle coste, dalla struttura dei polmoni, alle bolle di sapone...
E la panoramica rivela in tutti questi casi delle caratteristiche comuni, la prima delle quali è che le figure geometriche che vengono prodotte posseggono la proprietà di autosomiglianza (self-similarity), vale a dire che ogni piccola parte dell’oggetto è una immagine ridotte dell’oggetto intero.
(Se state cominciando a stancarvi di ripercorrere la zoomata delle potenze di dieci citate nel precedente post, potete già iniziare a divertirvi con un’altra zoomata, praticamente infinta: quella in un frattale).
Il termine dimensione frattale è la generalizzazione di concetti matematici introdotti da diversi autori, e indica dimensioni che possono prendere valori non interi: così una linea può avere una dimensione di 1,3 o una superficie avere dimensione 2,4.
Semplifico molto con un esempio: la curva di Peano è una curva che per il suo particolare tragitto riesce a percorrere tutti i punti in un piano, arrivando così ad essere qualcosa più di una linea (una dimensione) e qualcosa meno di un piano vero e proprio (due dimensioni).
Per maggiori chiarimenti sugli aspetti matematici (che spalancano le porte dello sguardo nel mondo, e non sono poi così irraggiungibili) consiglio di visitare alcuni siti introduttivi come quello estremamente chiaro dell’Università degli Studi di Milano (progetto METIS), composto da una sequenza di 27 “diapositive” con i testi di Salvinien Cyrano. Se non vi bastasse, altri siti con sezioni introduttive ma con anche molti approfondimenti sono quello di Laura Lotti, e quello ben curato di Terragni-Miorelli-Gariboldi. In inglese potete trovare l’introduzione a cura di Paul Bourke.
Infine però quel che salta all’occhio, quel che più ci interessa qui, è la visione di Mandelbrot, che supera e rinnova il panorama della geometria utilizzando materiale d’alta qualità, fino ad allora scartato per non aver trovato una applicazione.
Questa piccola (o grande?) rivoluzione ha avuto possibilità d’esistere sia grazie allo sguardo unificante di Mandelbrot, sia grazie allo sviluppo dei computer, che ha permesso di affrontare calcoli di verifica umanamente irraggiungibili, per lungo tempo solamente ipotizzati.
Ora, dopo le prime libere esplorazioni, l’ impiego dei frattali come modelli per lo studio dei fenomeni naturali si sta sviluppando in maniera più specifica: ogni “ex-mostro” viene utilizzato nell’ambito più adatto e sviluppate le sue potenzialità, raffinando lo strumento.
Ma il pensiero umano quotidiano, non avendo le potenzialità di calcolo di un computer, userà sempre solo paragoni con le forme euclidee? Forse, chissà, andando nel particolare e continuando a riferirci a cerchi e sfere, attuiamo inconsapevolmente qualche formula frattale tipo quella di Apollonio di Perga che riempie un piano di cerchi sempre più piccoli arrivando a un merletto o setaccio di cui la superficie si può dire nulla ma lo svolgimento lineare infinito.
20030518
Ad ognuno la sua scala (i meravigliosi Eames)
Permalink (da utilizzare per segnalare questo post)

Saper immaginare, non tanto per inventarsi qualcosa di non esistente, ma per riuscire a vedere ciò che non si può semplicemente guardare, è una capacità che può aiutare nella comprensione della realtà che ci circonda, nella previsione di accadimenti in nuce, nella valutazione del valore e della dimensione delle cose, nella crescita sociale.
Tra settembre 2002 e gennaio 2003 alla XX Esposizione Internazionale della Triennale di Milano è stata presentata una retrospettiva sul lavoro e sull'eredità lasciata da Charles Eames e dalla moglie Ray: “L'opera di Charles e Ray Eames. A Legacy of Invention”. Per comprendere pienamente le loro realizzazioni bisogna conoscere alcune delle sfide che essi si erano prefissati:
- come produrre mobili economici ma di alta qualità;
- come realizzare spazi abitativi o di lavoro economici e al tempo stesso ben disegnati;
- come aiutare la gente a cogliere la bellezza nella vita quotidiana;
- come aiutare gli Americani e le altre culture a capirsi reciprocamente;
- come rendere accessibili ai profani essenziali principi scientifici.
Già citando i titoli delle sezioni della retrospettiva che sta girando il mondo - arredo, spazio, bellezza, cultura e scienza - si può intuire la dimensione della loro opera. Due grandi innovatori.
Saper vedere, saper anche indicare agli altri. Ecco che scopriamo tra le loro opere una serie di video e filmati realizzati per la divulgazione scientifica. Uno di essi si intitola “Power of Ten” edito in Italia da Zanichelli (per la rivista "Le scienze" col titolo "Potenze di dieci", anche in versione cartacea).
Lo sguardo sincronico sul reale a diverse distanze non può che spingere a vedere ogni cosa come relativa ad un’altra presente al tempo stesso e non immediatamente percepibile.
Il viaggio dalla scala umana a quella dell’Universo e da lì a tornare fino a spingersi alla dimensione delle particelle subatomiche, come una sezione o spaccato dell’esistente, è percorribile in diversi siti: dal più sofisticato Powersof10, con numerosi rimandi a bibliografie e studi paralleli, al più semplice e agile Quarks to Quasar (ambedue i siti utilizzano le immagini realizzate per il video degli Eames); in italiano troviamo una sezione del sito Microcosmos del CERN, e il sito dai toni più didattici a cura di Linguaggio Globale editore on line. Infine una versione animata che oserei dire entusiasmante (per chi ha una connessione veloce) la si può trovare sul sito dedicato alla microscopia Molecular Expressions.
20030506
Attorno a noi come... ?
Permalink (da utilizzare per segnalare questo post)
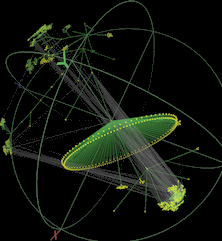
Walrus - Graph Visualization Tool
C’è un racconto di Dino Buzzati in cui un principe decide di esplorare il proprio regno fino a raggiungerne i confini. Il principe decide di prendere con sé sette messaggeri e di mantenere il contatto con il proprio castello tramite spedizioni di lettere dalle scadenze precise. Il racconto si intitola “I sette messaggeri” e si conclude con il principe che, non avendo trovato ancora i confini del proprio regno, decide di iniziare ad inviare i messaggeri non più ai propri cari (che ormai dispera di rivedere, tanto si è spinto lontano), bensì di inviarli in avanti, ad anticipare la sua ricerca, ricevendo così messaggi da quelle terre che andrà ad esplorare.
La visione del mondo che ci circonda, la concezione che abbiamo di esso e la forma che immaginiamo abbia, è qualcosa che di per sé può apparire pura speculazione filosofica o matematica, in realtà è la composizione in modo organizzato di un intero sistema di pensiero che può influenzare anche in modo diretto le nostre azioni e decisioni nel mondo reale.
Quasi superfluo (ma lo faccio per fissare ulteriori connessioni) citare quanto possa incidere sul quotidiano pensare di essere al centro dell’universo o immaginarsi su un piccolo pianeta parte di un sistema solare che è uno dei tanti, un po’ ai margini, tutto sommato “a lato”.
O pensare la geometria delle cose secondo riferimenti Euclidei o secondo le intuizioni di Mandelbrot e i sui frattali.
Ma se pensate che queste cose che scrivo siano proprio in un altro universo rispetto al modo in cui normalmente si porta avanti un discorso, andate a visitarvi il sito www.mappedellarete.net a cura di Giuliano Gaia e Stefania Bojano (che è la versione italiana di cybergeography di Martin Dodge).
I due siti sono una raccolta non solo delle principali mappature della rete internet, ma anche delle proposte di sistemi di mappatura di ipertesti, idee, gruppi di pensieri, collegamenti economici, galassie aziendali...
Le mappature, suddivise per categorie, sono moltissime e nella maggior parte di una bellezza sorprendente (non solo esteticamente). Il sito italiano le raggruppa in: artistiche, concettuali, geografiche, infospazi 2d, infospazi 3d, mappe di navigazione, mappe di siti e mappe topologiche (interessante nel sito di Dodge la sezione mappe storiche, dove si trovano i primi tentativi di dare forma a quel che non era ancora internet ma si chiamava Arpanet...). In ogni sezione sono segnalati e linkati gli studi più interessanti con affiancata una immagine di riferimento. Attraverso i link (dove si trovano programmi, video, rappresentazioni esemplificative...) c’è veramente da perdersi in una vastità che ci pare quasi di afferrare ma che ci sfugge, rivelandosi ogni volta più complessa di quanto si pensi.
20030505
Quel che poi un Metal Detector...
Permalink (da utilizzare per segnalare questo post)
Poi la notte, in quelle poche ore in cui l’aereoporto rimane chiuso, in cui le grandi sale restano completamente sgombre e gli altoparlanti restano silenziosi, i metal detector stanno come monoliti in fila e raccontano.
Fra di loro si passano le descrizioni degli oggetti che hanno potuto osservare; solo dei più interessanti, naturalmente.
Gruppi di oggetti, intere valige osservate come ritratti di persone, insiemi di abiti come catene di eventi; i metal detector hanno la capacità di selezionare e mettere in connessione tutto quel che vedono scoprendo trame di racconti insospettabili, pensieri celati, addirittura idee a venire.
Possono segnalare quel che viene chiesto loro di scovare, ma una quantità enorme di oggetti vengono vagliati e notati e taciuti perché non richiesti. Ma quel che poi un metal detector sa, scorre come racconto lungo la muta fila di pannelli, la sera, in quelle poche ore.
Per questo blog cercherò di essere un po’ come uno di questi metal detector. Con l’unica grande differenza che anziché stare immobile e aspettare che le cose passino tra le mie maglie con una casualità legata ai loro percorsi, sarò io ad andare in esplorazione, lasciando che tra i miei denti si fermino immagini e parole come plancton tra i fanoni delle balene.
Metal Detector
Permalink (da utilizzare per segnalare questo post)
Il metal detector, come dire che la radiografia dei bagagli delle persone o l'indagine sotto il pelo della terra...
|
|
| |
|
|
|